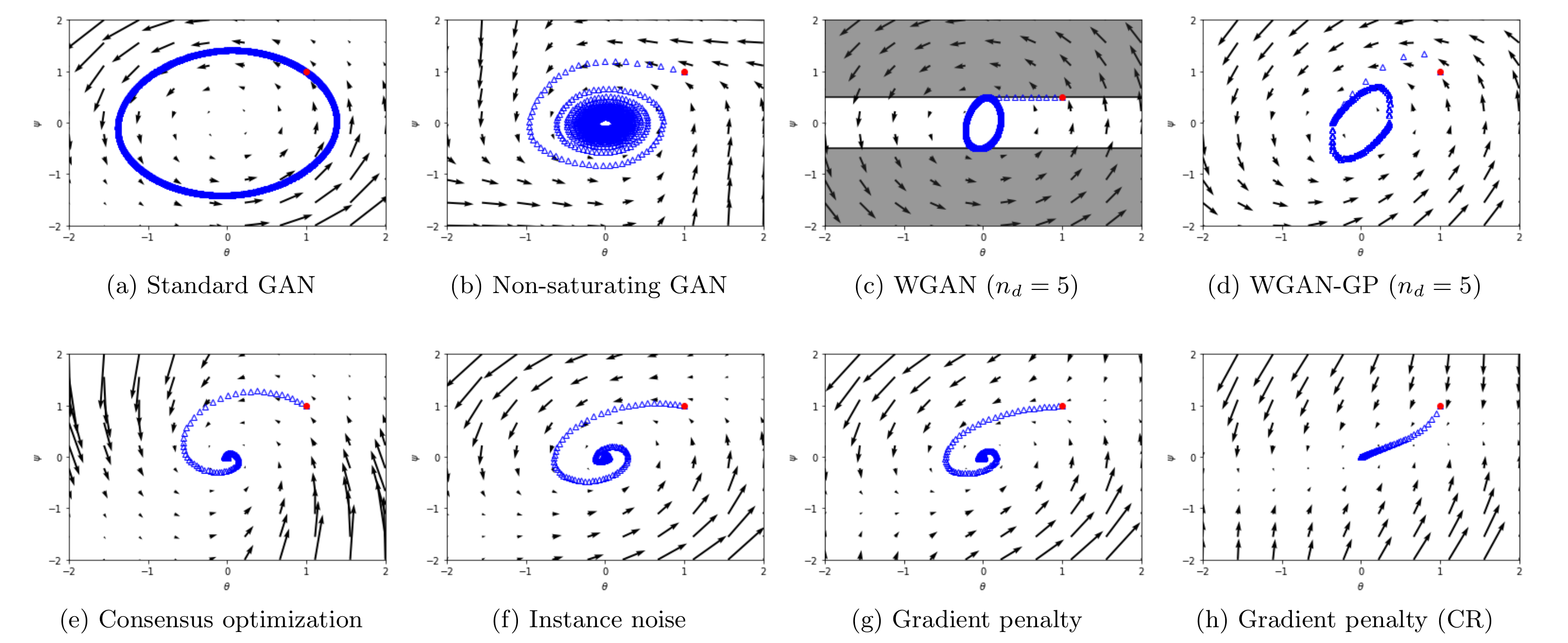
Convergence properties of different GAN training algorithms using alternating gradient descent for the Dirac-GAN. We see that whereas unregularized training of GANs and Wasserstein-GANs is not always convergent, training with instance noise or zero-centered gradient penalties leads to convergence.
Generative Adversarial Networks (GANs) are powerful latent variable models that can be used to learn complex real-world distributions. Especially for images, GANs have emerged as one of the dominant approaches for generating new realistically looking samples after the model has been trained on some dataset. However, while very powerful, GANs can be hard to train and in practice it is often observed that gradient descent based GAN optimization does not lead to convergence.
In this project, we analyze the stability of the GAN training dynamics using tools from discrete contol theory [ ]. We theoretically show that the main factors preventing state-of-the-art algorithms from converging are the presence of eigenvalues of the Jacobian of the associated gradient vector field with zero real-part and eigenvalues with a large imaginary part [ ]. This enables us to characterize the convergence properties of various training methods for GANs and derive new training methods that have better convergence properties [ ]. Empirically, we find our training methods to work well in practice and use them to learn high-resolution generative image models for a variety of datasets, including a generative model for all 1000 imagenet classes and a generative model for the celebA-HQ dataset at resolution 1024×1024, with little hyperparameter tuning.
