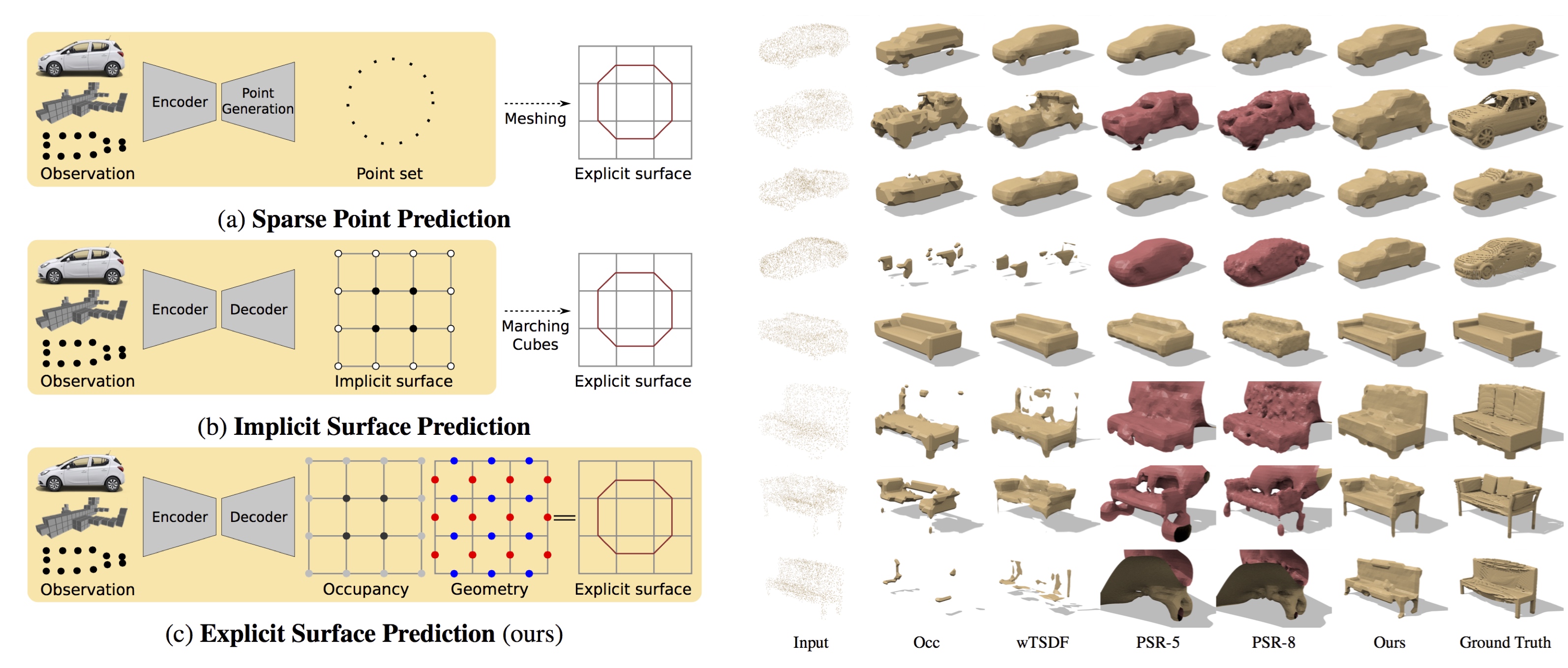
Left: Illustration comparing point prediction (a), implicit surface prediction (b) and explicit surface prediction (c). Right: 3D Shape Prediction from Point Clouds. Surfaces are colored: the outer surface is yellow, the inner is red.
Existing learning based solutions to 3D surface prediction cannot be trained end-to-end as they operate on intermediate representations (e.g., TSDF) from which 3D surface meshes must be extracted in a post-processing step (e.g., via the marching cubes algorithm). In this paper, we investigate the problem of end-to-end 3D surface prediction. We first demonstrate that the marching cubes algorithm is not differentiable and propose an alternative differentiable formulation which we insert as a final layer into a 3D convolutional neural network. We further propose a set of loss functions which allow for training our model with sparse point supervision. Our experiments demonstrate that the model allows for predicting sub-voxel accurate 3D shapes of arbitrary topology. Additionally, it learns to complete shapes and to separate an object's inside from its outside even in the presence of sparse and incomplete ground truth. We investigate the benefits of our approach on the task of inferring shapes from 3D point clouds. Our model is flexible and can be combined with a variety of shape encoder and shape inference techniques.
The code of our CVPR2018 paper can be found at http://www.cvlibs.net/redirect.php?site=deep_marching_cubes.
The data of our CVPR2018 paper can be found at http://www.cvlibs.net/download.php?file=deep_marching_cubes_data.zip.
